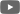
09 Juli Wie Wellen Informationen übertragen
Egal ob man mit Ultraschall den Körper untersucht, mit Radaranlagen den Luftraum, oder mit seismischen Wellen das Innere unseres Planeten: Wellen werden von ihrer Umgebung abgelenkt, gestreut oder reflektiert. Dadurch tragen diese Wellen dann eine gewisse Information über ihre Umgebung, und diese Information gilt es dann möglichst umfassend und präzise zu extrahieren. An der TU Wien gelang es nun, die Information, die eine Welle über ihre Umgebung mit sich trägt, mathematisch präzise zu beschreiben. Dadurch konnte gezeigt werden, wie Wellen überhaupt Informationen über ein Objekt aufnehmen und diese dann zu einem Messgerät transportieren.
Wo genau befindet sich die Information?
„Die Grundidee ist ganz alltäglich: Man schickt eine Welle auf ein Objekt, und der von dem Objekt zurückgestreute Teil der Welle wird an einem Detektor gemessen“, sagt Professor Stefan Rotter vom Institut für Theoretische Physik der TU Wien. „Aus den Messdaten kann man dann etwas über das Objekt lernen – zum Beispiel über seine präzise Position, Geschwindigkeit oder Größe.“ Diese Information über die Umgebung, die diese Welle mit sich trägt, bezeichnet man als ‚Fisher Information‘.
Üblicherweise gelangt nur ein Teil der Welle in den Detektor. Das wirft die Frage auf: Wo genau befindet sich diese Information in der Welle eigentlich? Mit dem neuentwickelten Formalismus konnte das Forschungsteam nun genau berechnen, an welchem Punkt des Raumes die Welle wieviel Information über das Objekt tatsächlich mit sich trägt. Dabei stellt sich heraus, dass die Information über unterschiedliche Eigenschaften des Objekts – wie Position, Geschwindigkeit und Größe – in ganz verschiedenen Teilen der Welle verborgen liegen kann.
„Um diesen Fragen auf den Grund zu gehen, sahen wir uns die mathematischen Eigenschaften dieser Fisher-Information näher an und kamen zu erstaunlichen Ergebnissen“, sagt Rotter. „Die Information erfüllt eine sogenannte Erhaltungsgleichung – die Information in der Welle bleibt bei der Bewegung durch den Raum erhalten, nach ganz ähnlichen Gesetzen, wie man das zum Beispiel auch für die Erhaltung der Energie kennt.“
Wie die theoretischen Berechnungen zeigen, hängt der Informationsgehalt der Welle genau davon ab, wie stark die Welle von den gesuchten Objekteigenschaften beeinflusst wird. „Wenn wir zum Beispiel messen wollen, ob sich ein Objekt etwas weiter links oder etwas weiter rechts befindet, dann wird die Fisher-Information genau von dem Bereich der Welle getragen, der mit der rechten und der linken Kante des Objektes in Berührung kommt“, sagt Jakob Hüpfl, der maßgeblich beteiligte Doktorand an der Studie. Diese Information breitet sich dann aus, und je mehr von dieser Information im Detektor ankommt, umso präziser kann man die Position des Objekts daraus ablesen.“
Experimentelle Bestätigung mit Mikrowellen
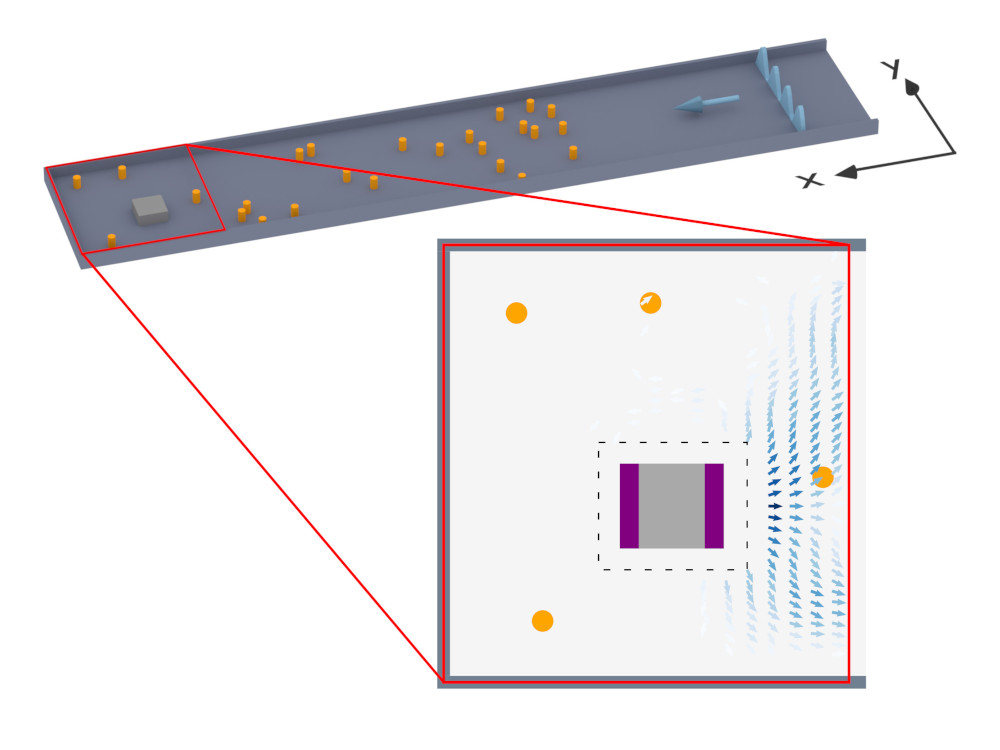
An der Universität Cote d’Azur in Nizza wurden in einer Mikrowellen-Kammer mithilfe zufällig positionierter Teflon-Objekte eine ungeordnete Umgebung erzeugt. Zwischen diesen Objekten befand sich ein metallisches Rechteck, dessen Position bestimmt werden sollte. Durch exakte Vermessung des Mikrowellenfelds konnte man genau zeigen wie die sich Information über die horizontale und die vertikale Position des Rechtecks ausbreitet: Sie geht von den jeweiligen Kanten des Rechtecks aus und bewegt sich dann mit der Welle mit – ohne, dass dabei Information verloren geht – genauso wie das von der neu entwickelten Theorie vorhergesagt worden war.

Experiment an der Université Côte d’Azur, Nizza: Ein Signal wird in den Wellenleiter injiziert, Weiße Zylinder, an denen die Welle gestreut wird, sorgen für ein komplexes Wellenfeld, dessen Informationsfluss analysiert wird. Bild: Université Côte d’Azur
Anwendungsmöglichkeiten in vielen Bereichen
„Diese neue mathematische Beschreibung der Fisher-Information hat das Potenzial, die Qualität ganz unterschiedlicher bildgebender Verfahren zu verbessern“, sagt Rotter. Wenn man quantifizieren kann, wo sich die gewünschte Information befindet und wie sie sich ausbreitet, kann man etwa den Detektor passend positionieren, oder maßgeschneiderte Wellen berechnen. Rotter erklärt: „Wir liefern damit einfache Formeln, mit denen man Mikroskopie-Methoden genauso verbessern kann wie quantenphysikalische Sensoren.“
Originalpublikation:
[Hüpfl, J., Russo, F., Rachbauer, L.M. et al. Continuity equation for the flow of Fisher information in wave scattering. Nat. Phys. (2024). https://doi.org/10.1038/s41567-024-02519-8]
Quelle und Bild: www.tuwien.at